Table of Contents
- Introduction
- Quantifying Uncertainty
- Significant Figures
- Experimental Errors
- Accuracy and Precision
- Propagation of Uncertainties
Introduction
-
Taking measurements of physical quantities such as length and mass is an integral part of any physical experiment.
-
To make measurements of different physical quantities, we use different instruments. For example, to measure length, we can use a ruler and to measure time, we use a clock, etc.
-
All measurements come with errors and uncertainties. These terms will be defined in subsequent sections.
Quantifying Uncertainty
-
In this section, we illustrate the process by which we quantify uncertainty in a physical measurement using the simplest case of a metre rule.
-
The simplest instrument for measuring length is the metre rule.
-
A reading is the single determination of a value at one point on the metre rule.
-
Typically, the smallest division of the rule is $0.1~$cm or $1~$mm.
-
Any reading can be estimated to within half of the smallest division. We call this the uncertainty associated with the reading. In this case, the uncertainty is $\frac{0.1}{2} = 0.05~$cm or $0.5~$mm.
The uncertainty in a reading is $\pm$ half of the smallest division in the measuring instrument.
- However, to measure the length of an object, two readings are needed - one at each end. Therefore, the uncertainties add and we deduce that the uncertainty associated with the measurement is $0.05~$cm + $0.05~$cm $=0.1~$cm or $1~$mm.
Table: Uncertainty in using the metre rule.
| The Metre Rule | cm | mm |
|---|---|---|
| Smallest Division | 0.1 | 1 |
| Uncertainty in Reading | $\frac{0.1}{2}=0.05$ | $\frac{1}{2}=0.5$ |
| Uncertainty in Measurement | $0.05\times 2=0.1$ | $0.5\times 2=1$ |
The uncertainty in a reading must be stated to one significant figure.
The reading must be quoted to the same number of decimal places as the uncertainty.
Estimate the reading shown in the following figure (numbers in cm).
Solution (click to expand)
$$ \text{Smallest division} = 0.1~\text{cm}.$$ $$ \text{Uncertainty in reading} = \frac{0.1}{2} = 0.05~\text{cm}.$$ Note that the reading lies somewhere between $32.3~$cm and $32.4~$cm.The average of these two values is simply $$\frac{32.3+32.4}{2}=32.35~\text{cm}$$. Therefore, $$ \text{Estimated reading} = 32.35 \pm 0.05~\text{cm}.$$
The uncertainty in a reading must be stated to one significant figure.
The reading must be quoted to the same number of decimal places as the uncertainty.
Estimate the reading shown in the following figure (numbers in cm).
Solution (click to expand)
$$ \text{Smallest division} = 0.2~\text{cm}.$$ $$ \text{Uncertainty in reading} = \frac{0.2}{2} = 0.1~\text{cm}.$$ Note that the reading lies somewhere between $23.2~$cm and $23.4~$cm.The average of these two values is simply $$\frac{23.2+23.4}{2}=23.3~\text{cm}$$. Therefore, $$ \text{Estimated reading} = 23.3 \pm 0.1~\text{cm}.$$
The uncertainty in a reading must be stated to one significant figure.
The reading must be quoted to the same number of decimal places as the uncertainty.
Estimate the length of the object shown in the following figure.
Solution (click to expand)
$$ \text{Left reading} = 1.40 \pm 0.05 \text{cm}$$ $$ \text{Right reading} = 6.75 \pm 0.05 \text{cm}$$ $$ \begin{align*} \text{Length of object} &= (6.75 - 1.40) \pm (0.05+0.05 ) \\ &= 5.4\pm 0.1~\text{cm} \end{align*} $$The uncertainties add even though the readings are subtracted.
Significant Figures
-
In many cases, the uncertainty of a number is not stated explicitly. Instead, the uncertainty is indicated by the number of meaningful digits, or significant figures, in the measured value.
-
For example, a stopwatch reading of $1.2~$s (two significant figures) is less precise than a reading of $1.23~$s (three significant figures).
-
To deduce the number of significant figures in a reported result, we recall the rules outlined in the following table:
| Result | Significant Figures | Rule | Scientific Notation |
|---|---|---|---|
| $302$ | $3$ | Zeros between two non-zero digits are significant | $3.02\times 10^2$ |
| $320$ | $2$ | Trailing zeros in an integer with no decimal shown are NOT significant. | $3.2\times 10^2$ |
| $320. $ | $3$ | Trailing zeros in an integer with the decimal shown are significant. | $3.20\times 10^2$ |
| $0.000203$ | $3$ | Leading zeros are NOT significant. | $2.03\times 10^{-4}$ |
| $0.005200$ | $4$ | Trailing zeros to the right of the decimal are significant. | $5.200\times 10^{-3}$ |
| $100.02$ | $5$ | Zeros between two non-zero digits are significant | $1.0002\times 10^2$ |
- When we work with very large or very small numbers, we can show significant figures much more easily by using scientific notation, sometimes called powers-of-10 notation.
A number expressed in scientific notation is given by:
$\boxed{a \times 10^b}$
where $1\leq |a| < 10$ is called the mantissa and $b$ is an integer called the exponent. The number of significant figures is the number of digits in $a$.Give the number of significant figures in each measurement and express each in scientific notation. $$\text{(a)}~26.8~\text{m} \qquad ~\text{(b)}~0.004506~\text{s} \qquad ~\text{(c)}~3002~\text{kg} \qquad ~\text{(d)}~102,560,000~\text{m/s}$$
Solution (click to expand)
Computations with Significant Figures
-
When we use numbers with uncertainties to compute other numbers, the computed results are also uncertain.
-
In other words, when we perform operations on measured values (with a certain number of significant figures), how many significant figures should the results have?
Calculations with Significant Figures
- In multiplication or division of two numbers, or taking root or power of a number, the result must have as many significant figures as the least precisely known number entering the calculation.
- In addition and subtraction, the number of decimal digits in the answer must be equal to the least number of decimal places in the numbers added or subtracted.
Compute each of the following. $$\text{(a)}~3.21 + 2.1 \qquad ~\text{(b)}~ 13.276 - 5.31 $$
Solution (click to expand)
Compute each of the following and express in scientific notation. $$\text{(a)}~24\times 296 \qquad ~\text{(b)}~ \frac{5.342}{2.34} \qquad ~\text{(c)}~10.3^3 \qquad ~\text{(d)}~ \sqrt{78900}$$
Solution (click to expand)
Experimental Errors
An error is the difference between a measured result and the true value, i.e. the value that would have been obtained in an ideal measurement.
- Errors can be classified as random or systematic and an error of unknown size is a source of uncertainty.
Random Errors
-
Random errors produce unpredictable deviations from the actual value such that each reading has an equal chance of falling above or below the actual value.
-
Random errors cannot be eliminated but can be reduced by finding the average of all the readings obtained.
Systematic Errors
-
Systematic errors produce readings that are predictably distributed in the same direction, e.g. either above or below the actual value, too large or too small.
-
Systematic errors can be minimized by taking sensible precautions, such as checking for zero errors and avoiding parallax errors.
Figure - Systematic error resulting from parallax error of the experimenter. |
Figure - Systematic error resulting from zero error of an ammeter. This type of error can be reduced by re-calibrating the ammeter. |
Accuracy and Precision
-
Accuracy refers to the closeness of the measured value to the true value. A measurement is said to be accurate if the systematic error is small.
-
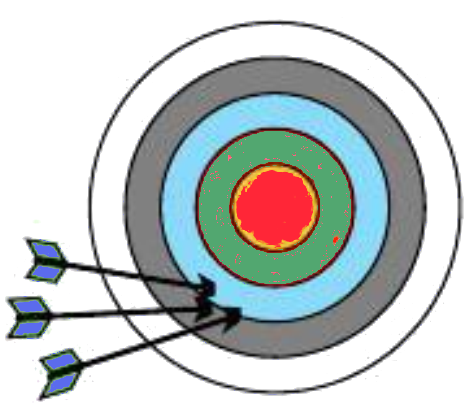
Precision refers to how close a set of measured values are to each other. A measurement is said to be precise if the random error is small.
|
Figure - Arrows on a target. Precise but not accurate. |
Table - Accuracy vs Precision.
| digitalblackboard.io | ACCURATE (Small Systematic Error) |
NOT ACCURATE (Large Systematic Error) |
| PRECISE (Small Random Error) |
||
| NOT PRECISE (Large Random Error) |
Propagation of Uncertainties
-
A measurement of a length may be quoted as $L= (18.6 ± 0.2)~$cm where the value $18.6~$cm is the best estimate or the mean value of the measurement and $0.2~$cm is called the uncertainty in the measurement.
-
Although the uncertainty is a useful quantity, it is important to know how this quantity compares with the quantity measured. To this end, we introduce two new terms called the fractional uncertainty and percentage uncertainty.
If a quantity is measured as $x=x_0 \pm \Delta x$, the fractional uncertainty is defined as:
$\boxed{\text{Fractional Uncertainty}=\frac{\Delta x}{x_0} }$
and the percentage uncertainty is defined as:$\boxed{\text{Percentage Uncertainty}=\frac{\Delta x}{x_0} \times 100\\\% }$
- In the above example $L= (18.6 ± 0.2)~$cm, we have: $$\text{Uncertainty} = 0.2~\text{cm}$$ $$\text{Fractional uncertainty} = \frac{0.2}{18.6} =0.0108 $$ $$\text{Percentage uncertainty} = 0.0108\times 100\% \approx 1\%$$
Unless otherwise stated, both uncertainty and percentage uncertainty should be stated to 1 significant figure.
Addition and Subtraction
Uncertainty of Sum or Difference
The uncertainty of a sum or difference of 2 quantities $x$ and $y$ is the sum of the uncertainties of the 2 quantities.:
$\boxed{r=x\pm y \implies \Delta r = \Delta x + \Delta y }$
The lengths $a$ and $b$ are $(4.2\pm 0.1)~$cm and $(5.5\pm 0.1)~$cm, respectively. Find the percentage uncertainty of $s$ and $t$ where $$\text{(a)}~s=a+b \qquad ~\text{(b)}~t=3a-2b$$
Solution (click to expand)
- $s=4.2+5.5=9.7~$cm.
$\Delta s=0.1+0.1=0.2~$cm.
$$
\begin{align*}
\text{Percentage uncertainty of} ~s &= \frac{\Delta s}{s} \times 100\% \\
&= \frac{0.2}{9.7} \times 100\% \\
&= 2\%
\end{align*} $$
Multiplication and Division
Uncertainty of Product or Quotient
The fractional uncertainty of a product or quotient of 2 quantities $x$ and $y$ is the sum of the fractional uncertainties of the 2 quantities.:
$\boxed{r=xy \quad \text{or} \quad r=\frac{x}{y} \implies \frac{\Delta r}{r} = \frac{\Delta x}{x} + \frac{\Delta y}{y}}$
Two lengths are reported as $x=18.5\pm 0.5~$mm and $y=12.5\pm 0.5~$mm. Compute $r=xy$ and $s=\frac{x}{y}$, stating clearly the corresponding uncertainty.
Solution (click to expand)
The dimensions of a piece of cardboard are $x=297\pm 1~$mm and $y=209\pm 1~$mm. Compute
(a) the percentage uncertainty of $x$.
(b) the area $xy$ with its uncertainty.
Solution (click to expand)
The thin lens formula is given by: $$\frac{1}{f} = \frac{1}{u} + \frac{1}{v}$$ where $u=(50\pm 3)~$mm and $v=(200\pm 5)~$mm and the value of $f$ is shown to be $40~$mm. Determine the uncertainty of $f$.
Solution (click to expand)
Powers and Roots
Uncertainty of Power or Root
The fractional uncertainty of a rational exponent is the product of the exponent and the fractional uncertainty of the base:
$\boxed{r=x^n \implies \frac{\Delta r}{r} = n\frac{\Delta x}{x} }$
The period $T$ of a satellite is dependent on its radius $r$ of the orbit but independent of its mass and can be represented by the equation: $$T = 2\pi\sqrt{\frac{r^3}{GM}}$$ $$\text{where} \begin{cases} r~\text{is the radius of the orbit.}\\ G~\text{is the gravitational constant with unit Nkg$^{-2}$m$^2$.}\\ M~\text{is the mass of the Earth.} \end{cases}$$ If the percentage uncertainties of $T$ and $M$ are $\pm 3~$% and $\pm 4~$%, respectively, what will be the percentage uncertainty of $r$?
Solution (click to expand)
In an experiment to determine the viscosity $\eta$ of a liquid, the following equation was used: $$\eta = \frac{kr^2}{v}$$ $$ \text{where} \begin{cases} r=(0.83 \pm 0.01)~\text{mm}\\ v=(0.065 \pm 0.002)~\text{ms}^{-1}\\ k~\text{is a constant with value}~93.7~ \text{Nm}^{-3}. \end{cases}$$ Compute the value of $\eta$ with its corresponding uncertainty.