Table of Contents
Scalars
-
Some quantities in physics, such as time, distance, mass, speed and temperature, just need one number to specify them. These are called scalar quantities.
-
For example, it is sufficient to say that the mass of a body is 52 kg or that the temperature is 25.0 $^{\circ}$C.
Scalars are quantities that have magnitude only.
Table: Some scalar quantities (with SI unit).
| Scalar Quantity | SI Unit | Symbol |
|---|---|---|
| Time | s | $t$ |
| Mass | kg | $m$ |
| Density | kg/m$^3$ | $\rho$ |
| Distance | m | $d$ |
| Speed | m/s | $s$ |
| Energy | J | $E$ |
| Power | J/s | $P$ |
| Electric Charge | C | $q$ |
| Current | A | $I$ |
- Scalars may be added by simple arithmetic.
Which list contains only scalar quantities?
A mass, acceleration, temperature, kinetic energy
B mass, volume, electric potential, kinetic energy
C acceleration, temperature, volume, electric charge
D moment, electric field, density, magnetic flux
Solution (click to expand)
B
Vectors
-
Some quantities are fully specified only if, in addition to a number, a direction is also given.
-
For example, saying that you are sitting in a car travelling at 120 km/h does not tell us where you will be in 10 minutes because we do not know the direction in which you are travelling. Therefore, we need to specify the velocity, instead of just the speed.
Vectors are quantities that have direction as well as magnitude.
Table: Some vector quantities (with SI unit).
| Vector Quantity | SI Unit | Symbol |
|---|---|---|
| Displacement | m | $\bm{s}$ |
| Velocity | m/s | $\bm{v}$ |
| Acceleration | m/s$^2$ | $\bm{a}$ |
| Force | N | $\bm{F}$ |
| Momentum | Ns | $\bm{p}$ |
| Moment | Nm | $\bm{M}$ |
| Electric field | V/m | $\bm{E}$ |
-
Vectors are denoted by boldface letters (e.g. $\bm{v}$, $\bm{a}$, $\bm{F}~$), or with an arrow cap (e.g. $\vec{v}$, $\vec{a}$, $\vec{F}~$) or with a tilde underneath (e.g. $\utilde{v}$, $\utilde{a}$, $\utilde{F}~$).
-
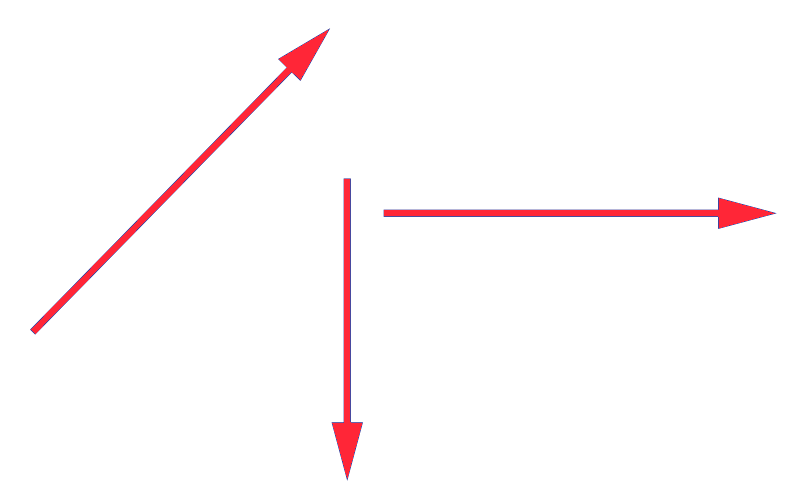
A vector is represented by a straight arrow as shown in the following figure. The direction of the arrow represents the direction of the vector and the length of the arrow represents the magnitude of the vector.
- The vectors in the following figure are all equal to each other. We therefore deduce that vectors do not have to start from the same point to be equal.
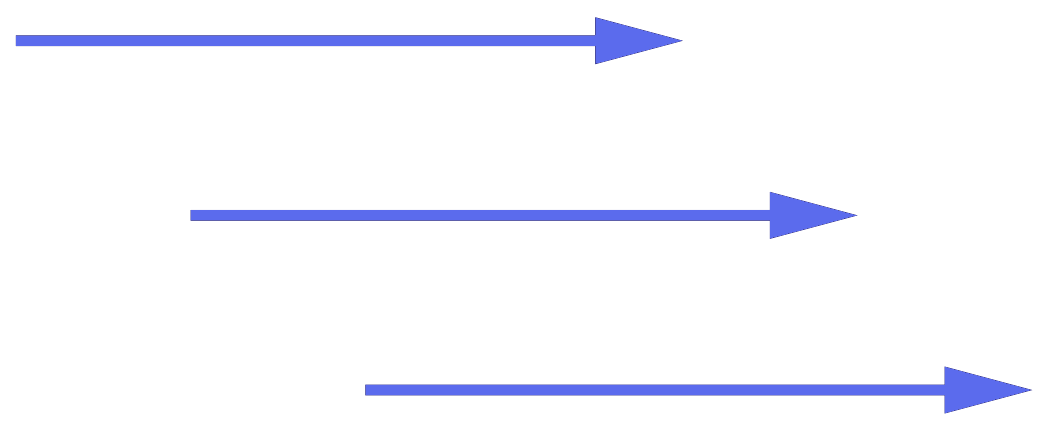
All vectors with the same magnitude and direction are equal.
- Every vector has an initial point and a final point where the direction is from the former to the latter. Let the initial point be denoted by $A$ and the final point be denoted by $B$, then an alternative symbol for the vector is $\overrightarrow{AB}$.
Magnitude of a Vector
- The magnituide of a vector $\bm{a}$ is given as either $a$ or $|\bm{a}|$.
Multiplication of a Vector by a Scalar
-
A vector can be multiplied by a number. The vector $\bm{a}$ multiplied by the scalar $2$ gives a vector in the same direction as $\bm{a}$ but $2$ times longer.
-
The vector $-\bm{a}$ has the same magnitude as $\bm{a}$ but is opposite in direction.The vector $\bm{a}$ multiplied by $−\frac{1}{2}$ is opposite to $\bm{a}$ in direction and half as long.
Addition of Vectors
-
In this article, we deal only with coplanar vectors which are vectors that lie in the same plane.
-
Given two vectors $\bm{a}$ and $\bm{b}$, we can add them in two ways - parallelogram law or triangle law for vector addition.
-
Parallelogram law for vector addition
- we can shift the two vectors so that the initial points coincide at $O$.
- the vectors $\bm{a}$ and $\bm{b}$ then form the sides of a parallelogram.
- the diagonal of the parallelogram is then the resultant vector $\bm{a} + \bm{b}$.
-
Triangle law for vector addition
- place the initial point of the second vector (i.e. $\bm{b}$) at the final point of the first vector (i.e. $\bm{a}$).
- construct the vector pointing from the initial point of $\bm{a}$ to the final point of $\bm{b}$. This vector is the resultant vector $\bm{a} + \bm{b}$.
-
Conversely, for the triangle law, we can also place the initial point of $\bm{a}$ at the final point of $\bm{b}$. The resultant vector $\bm{b} + \bm{a}$ constructed will be the vector pointing from the initial point of $\bm{b}$ to the final point of $\bm{a}$, which is identical to $\bm{a} + \bm{b}$.
-
this tells us that vector addition is commutative:
$$\boxed{\bm{a} + \bm{b} = \bm{b} + \bm{a} }$$
Subtraction of Vectors
-
Given two vectors $\bm{a}$ and $\bm{b}$, we wish to compute $\bm{a} - \bm{b}$. We realize that $~\bm{a} - \bm{b} = \bm{a} + (-\bm{b})$.
-
The above result tells us we can add $-\bm{b}$ to $\bm{a}$ using the triangle law. See Figure (b) below.
-
Further, according to our commutative law for vector addition, $\bm{a} + (-\bm{b}) = -\bm{b} + \bm{a}$. This means we can also add $\bm{a}$ to $-\bm{b}$ using the triangle law. See Figure (c) below.
Components of a Vector
-
Imagine we place a vector $\bm{a}$ on the Cartesian plane where the starting point of the vector coincides with the origin.
-
We define the components of the vector as the scalar projections of the vector on the axes.
Definition
The $x$- and $y$-components of a vector $\bm{a}$, called $a_x$ and $a_y$ are given by:
$\boxed{\begin{matrix} a_x = a\cos\theta \\ a_y = a\sin\theta \end{matrix} }$
where $\theta$ is the angle between the positive $x$-axis and the vector in a counter-clockwise direction.-
While the definition of the components of a vector are defined in terms of the standard angle $\theta$, it may sometimes be more convenient to work with the angle $\phi$ which is the acute angle between the vector and the $x$-axis.
-
For example, in the first quadrant, the angle $\phi$ is the angle between the vector and the positive $x$-axis. This coincides with the angle $\theta$. In the third quadrant, the angle $\phi$ is the angle between the vector and the negative $x$-axis.
Find the components of the vectors $\bm{a}$ and $\bm{b}$ in the following figure, given that the magniture of $\bm{a}$ is 16 units and that of $\bm{b}$ is 10 units.
Solution (click to expand)
Reconstructing a Vector from its Components
-
Why are we interested in the components of a vector? One reason is that knowing the components of a vector allows us to reconstruct it (i.e. finding its magnitude and direction).
-
Suppose that we are given that the $x$- and $y$-components of a vector $\bm{a}$ are $a_x$ and $a_y$. We need to find the magnitude $a$ of the vector and the angle $\theta$ it makes with the positive $x$-axis.
Magnitude and Direction of a Vector from its Components
Given the $x$- and $y$-components of a vector $\bm{a}$ are $a_x$ and $a_y$, the magnitude of $\bm{a}$ is given by:
$\boxed{a= \sqrt{a_x^2 + a_y^2}}$
and the angle $\theta$ is given by$\boxed{\theta= \tan^{-1}\left(\frac{a_y}{a_x}\right)}$
where $-\frac{\pi}{2} <\theta < \frac{\pi}{2}$ is the principal range of the $\tan^{-1}$ function.The second equation will give you the correct value of $\theta$ if the vector lies in the first quadrant. However, if the vector lies in the other quadrants, a more convenient way is to ignore the signs and the formula will then give the acute angle between the vector and the $x$-axis ($\phi$). We can then infer the value of $\theta$ with a sketch of the vector in its quadrant.
Given that the components of a vector $\bm{a}$ are $a_x=-4$ and $a_y=-2$, find its magnitude and the angle $\theta$ that the vector makes with the positive $x$-axis.
Solution (click to expand)
Calculating Vector Sum using Components
- The following figure shows two vectors $\vec{A}$ and $\vec{B}$ and their vector sum $\vec{R}$ together with their corresponding $x$- and $y$-components.
-
We observe from the figure that the $x$-component $R_x$ of the vector sum $\vec{R}$ is simply the sum $A_x + B_x$ which is the sum of the $x$-components of the vectors being added. The same holds true for the $y$-components. That is, $R_y = A_y + B_y$.
-
We can generalize the above observation and conclude that
Adding Vectors using Components
If $\vec{R}=\vec{A}+\vec{B}+\vec{C}+\cdots$, then the components of $\vec{R}$ are given by:
$\boxed{\begin{matrix} R_x = A_x + B_x + C_x + \cdots \\ R_y = A_y + B_y + C_y + \cdots \end{matrix} }$
We note that the above results also extend to vectors in 3-D space.- Once we have the components $R_x$ and $R_y$ of the vector resultant $\vec{R}$, we can readily compute its magnitude $R$ and direction $\theta$ using
$$ \begin{aligned} R &= \sqrt{R_x^2 + R_y^2} \\ \theta &= \tan^{-1}\left(\frac{R_y}{R_x}\right) \end{aligned} $$
Three vectors $\bm{a}$, $\bm{b}$ and $\bm{c}$ lying in the $x$-$y$ plane are shown in the following figure. The magnitudes of the vectors are: $a = 6$, $b = 4$ and $c = 7$. Find the magnitude and direction of the vector sum $\vec{R}$.