Table of Contents
Introduction
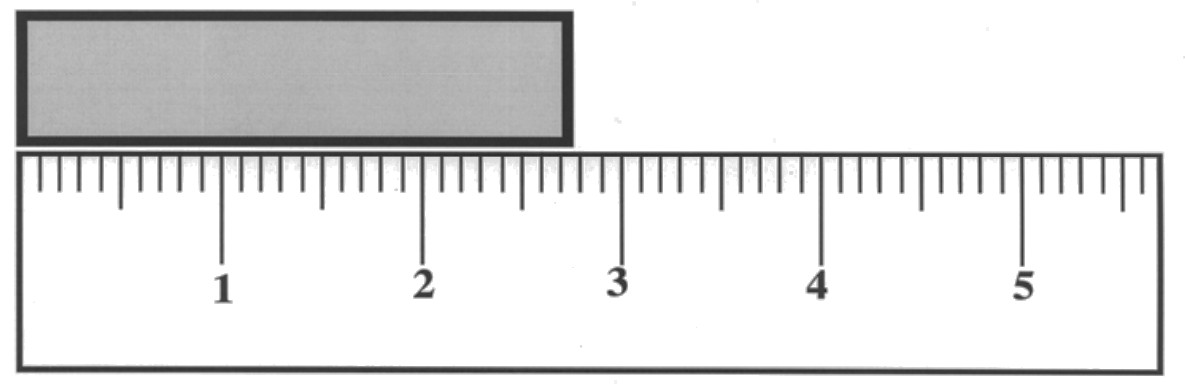
- In physics, quantities that can be measured are known as physical quantities. Two examples (length and mass) are shown in the following figures.
|
|
- All measurements are presented as a numerical value followed by a unit. In the above example, we have the following numerical values and units for length and mass.
| Physical Quantity | Numerical Value | Unit |
|---|---|---|
| Length | 2.75 | cm |
| Mass | 5.0 | kg |
S.I. Units
- In 1960, scientists at the General Conference of Weights and Measures adopted the International usage of a metric system of measurement called the Système International d’Unités (SI).
Base Units
- The S.I. system of units distinguishes seven physical quantities as base or fundamental quantities. These base quantities were chosen arbitrarily to be the building blocks of all physical quantities. Their corresponding units are called base units.
Table: Base quantities and units.
Derived Units
-
Many physical quantities are defined in terms of two or more base quantities.
-
A derived quantity is related to the base quantities through a defining equation. It can be expressed as the product or quotient (or a combination of products and quotients) of base quantities.
-
The derived unit is related to the base units in a similar manner as the derived quantity is related to the base quantities.
Write down the derived units of the following derived quantities (defining equation given).
| (a) $\displaystyle \text{Density} = \frac{\text{Mass}}{\text{Volume}}$ | (b) $\displaystyle \text{Velocity} = \frac{\text{Displacement}}{\text{Time}}$ |
| (c) $\displaystyle \text{Acceleration} = \frac{\Delta\text{ Velocity}}{\text{Time}}$ | (d) $\displaystyle \text{Force} = \text{Mass} \times \text{Acceleration}$ |
Solution (click to expand)
- Some derived quantities together with their deinitions, base/derived units are given in the following table.
Table: Derived quantities and units.
-
We see from the above table that certain derived units can be replaced conveniently by simpler names. For example, the derived unit of force is kgms$^{-2}$ which is replaced by the newton (N).
-
Base units are used to find units of unknown quantities in an equation.
-
The units of an unknown derived quantity in a physical equation can be found by substituting known units into the defining equation.
The effect of the resistive force on a moving car travelling with speed $v$ is given by the equation $$F = \frac{1}{2}C_D \rho A v^2 $$ where $C_D$ is the drag coefficient, $\rho$ is the density of air and $A$ is the cross-sectional area of the car. Show that $C_D$ is dimensionless.
Solution (click to expand)
The power, $P$ generated by an idea wind turbine is given by $$P =\frac{1}{2}k\rho (v-b)^3$$ $$\text{where} \begin{cases} k~\text{is a constant.}\\ \rho~\text{is the density of the fluid.}\\ v~\text{is the velocity of the fluid.} \end{cases}$$ What are the possible units of $k$ and $b$?
Solution (click to expand)
Prefixes
-
Many measurements are very much larger or smaller than the SI base unit.
-
In such cases, it is convenient to write these as multiples or sub-multiples of the base units using prefixes. For example, $1000$m is written as $1$km (kilometre) and $0.001$m is written as $1$mm (millimetre).
The resistance of a conductor is given by the equation $$R = \frac{V}{I}$$ where $V$ is in volts (v), $I$ is in ampere (A) and $R$ is in ohms ($\Omega$). Calculate the potential difference, $V$, needed for a current, $I$ of $25\mu$A to flow through a $2.2$k$\Omega$ resistor. Give your answer in mV.
Solution (click to expand)
Homogeneity of Equations
-
Base units can be used to check the homogeneity of a physical equation. This involves checking units on the left-hand and right-hand sides of the equation.
-
If the units are the same, then we say that the equation is homogeneous and dimensionally consistent.
-
However, this does not guarantee the equation is physically correct. There could be an incorrect coefficient, a missing or extra term, or a wrong positive or negative sign.
A student found four equations that describe how the velocity of ocean waves is related to the density of seawater $\rho$, the acceleration of free fall $g$, the depth of the ocean $h$ and the wavelength $\lambda$. $$v = \sqrt{g\lambda} \qquad v = \sqrt{\frac{g}{h}} \qquad v = \sqrt{\rho g h} \qquad v = \sqrt{\frac{g}{\rho}}$$ Which of these equations could be correct?
Solution (click to expand)
The period $T$ of the orbit around the Sun is given by $$T = 2\pi\sqrt{\frac{R^3}{GM}}$$ $$\text{where} \begin{cases} R~\text{is the radius of the orbit.}\\ G~\text{is the gravitational constant with unit Nkg$^{-2}$m$^2$.}\\ M~\text{is the mass of the Sun.} \end{cases}$$ Show that the equation is homogeneous in terms of base units.