Table of Contents
- Introduction
- The Concept of a Force
- Newton’s First Law of Motion
- The Concept of Mass
- The Concept of Weight
- The concept of Normal Reaction Forces
Introduction
-
We begin our study of dynamics by defining the concepts of force and mass.
-
Newton’s First Law of Motion (also called the Law of Inertia) states that an object at rest will remain at rest, and an object in motion will continue in a straight line at a constant speed, unless acted upon by an external force. This means that if there is no net force acting on an object, its velocity will not change.
The Concept of a Force
-
Dynamics is the study of the forces that cause objects and systems to move.
-
Our intuitive definition of a force is either a push or a pull. We know that a push or pull has both magnitude and direction. Therefore, a force is a vector quantity.
-
Since force is a vector, it adds just like other vectors, as illustrated in Figure 1 for two ice skaters. Forces are represented by arrows and can be added using the familiar triangle law or parallelogram law of vector addition.
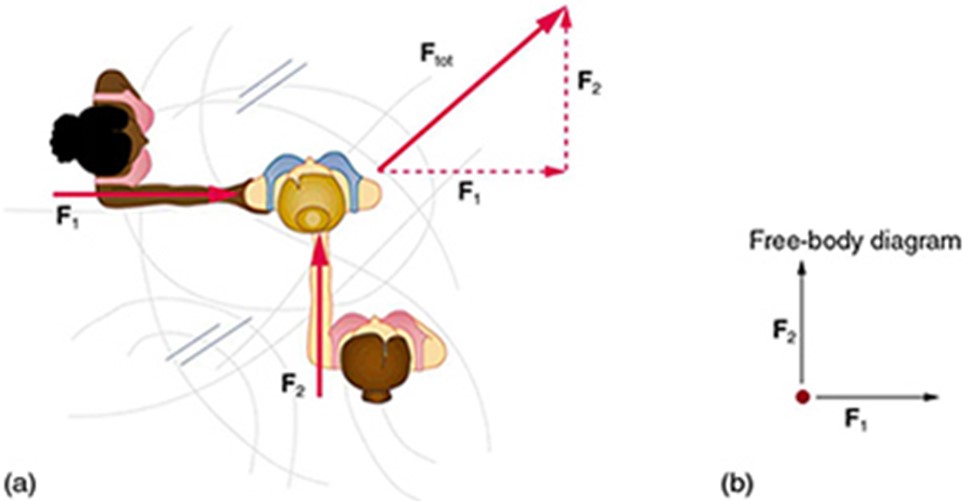
- Figure 1(b) is our first example of a free-body diagram, which is a technique used to illustrate all the external forces acting on a body. The body is represented by a single isolated point (or free body), and only those forces acting on the body from the outside (external forces) are shown.
Newton’s First Law of Motion
-
Experience suggests that an object at rest will remain at rest if left alone, and that an object in motion tends to slow down and stop unless some effort is made to keep it moving.
-
However, the above observations are in contrast to what Newton’s First Law of Motion states:
Newton's First LawA body at rest remains at rest, or, if in motion, remains in motion at a constant velocity unless acted on by a net external force.
-
Newton’s first law of motion states that there must be a cause (which is a net external force) for there to be any change in velocity (manifested as either a change in magnitude or direction).
-
An object sliding across a table or floor slows down due to the net force of friction acting on the object. If we spray the surface with talcum powder to make the surface smoother, the object slides farther. If we make the surface even smoother by rubbing lubricating oil on it, the object slides even farther. We can extrapolate the above observations and imagine the object sliding on a frictionless surface, the object will continue sliding in a straight line indefinitely.
-
Therefore, just as Newton’s first law predicts, if friction disappears and there is no net force acting on the object, it will continue sliding with a constant velocity indefinitely.
-
Newton’s first law is universally applicable and can be applied to anything from an object sliding on a table to a satellite in orbit to blood pumped from the heart. Experiments have thoroughly verified that any change in velocity (speed or direction) must be caused by an external force.
The Concept of Mass
-
The first law suggests that all matter has an in-built tendency to resist any change in its state of rest or uniform motion. This property of a body to remain at rest or to remain in motion with constant velocity is called its inertia. Therefore, Newton’s first law is often called the law of inertia.
-
As we know from experience, some objects have more inertia than others. It is obviously more difficult to change the motion of a large boulder than that of a basketball, for example. The inertia of an object is measured by its mass.
-
Mass is a measure of the amount of matter in an object which is determined by the numbers of atoms and molecules of various types it contains.
-
Unlike weight, mass does not vary with location. The mass of an object is the same on Earth, in orbit, or on the surface of the Moon. In practice, it is very difficult to count and identify all of the atoms and molecules in an object, so masses are not often determined in this manner. Operationally, the masses of objects are determined by comparison with the standard kilogram.
The Concept of Weight
-
The weight of a body is the result of the gravitational attraction between the mass $m$ of a body and the mass of the planet on which the body is placed. The weight of a body is given by the formula:
$$\boxed{ W = mg }$$
where $m$ is the mass of the body (kg), $g$ is gravitational field strength (N/kg) and weight is in Newton (N).
-
The gravitational field strength $g$ is also known as ’the acceleration due to gravity’ or the ‘acceleration of free fall’. On the surface of the Earth, $g= 9.80~$N/kg. The unit of $g$ is also m/s$^2$ as we have studied in the topic on kinematics.
-
The mass of an object is the same everywhere in the universe, but its weight depends on the location of the body. For example, a mass of 70 kg has a weight of 687 N on the surface of the Earth ($g=9.80~$N/kg) and a weight of $635~$N at a height of $250~$km from the Earth’s surface (where $g=9.07~$N/kg). However, on the surface of Venus, where the gravitational field strength is only $8.9~$N/kg, the weight is $623~$N.
The concept of Normal Reaction Forces
-
Weight is a pervasive force that acts at all times and must be counteracted to keep an object from falling. You definitely notice that you must support the weight of a heavy object by pushing up on it when you hold it stationary, as illustrated in Figure 2(a).
-
In Figure 2(b), the table supporting the load $\bm{w}$, must supply an upward force $\bm{N}$ equal to the weight of the load. This is so that the net external force on the load is zero and the load remains stationary in accordance with Newton’s First Law
-
If the force $\bm{N}$ supporting the load is perpendicular to the surface of contact between the load and its support, this force is defined to be a normal force and given the symbol $\bm{N}$.
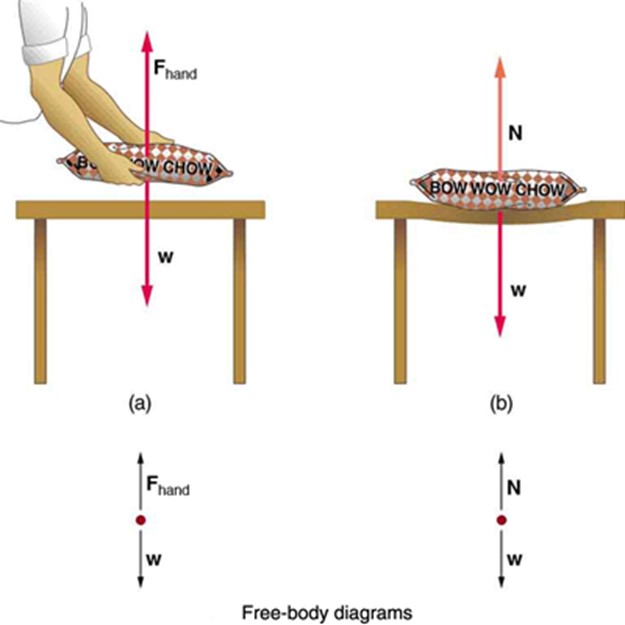
Figure 2 - (a) The person holding the object must supply an upward force $\bm{F}_\text{hand}$ equal in magnitude and opposite in direction to the weight of the object $\bm{w}$. (b) The table sags when the object is placed on it, much like a stiff trampoline. Elastic restoring forces in the table grow as it sags until they supply a force $\bm{N}$ equal in magnitude and opposite in direction to the weight of the load $\bm{w}$.
Figure 3 - Examples of normal forces.
Tension
-
A tension is a force along the length of a medium, especially a force carried by a flexible medium, such as a rope or cable.
-
Any flexible connector, such as a string, rope, chain, wire, or cable, can exert pulls only parallel to its length; thus, a force carried by a flexible connector is a tension with direction parallel to the connector. It is important to understand that tension is a pull in a connector. The tension force pulls outward along the two ends of a rope.
-
Consider a person holding a mass on a rope as shown in Figure 4.15.
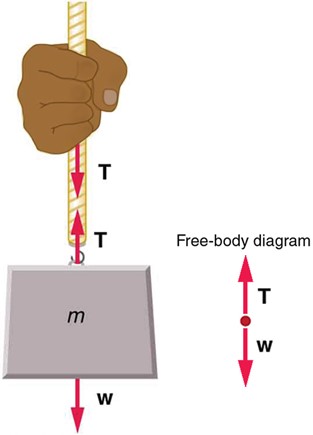
Figure 4 - When a perfectly flexible connector such as this rope transmits a force $\bm{T}$, that force must be parallel to the length of the rope. The pull such a flexible connector exerts is a tension. Note that the rope pulls with equal force but in opposite directions on the hand and the supported mass (neglecting the weight of the rope). This is an example of Newton’s third law. The rope is the medium that carries the equal and opposite forces between the two objects. The tension anywhere in the rope between the hand and the mass is equal. Once you have determined the tension in one location, you have determined the tension at all locations along the rope.