Table of Contents
Introduction
In this article, we will examine the inverses of the 3 basic trigonometric ufuncs:
| Function | Ufunc | Input x |
Domain of Function | Description |
|---|---|---|---|---|
| $\sin^{-1} x$ | np.arcsin(x) |
real | $-1 \leq x \leq 1$ | Inverse Sine function |
| $\cos^{-1} x$ | np.arccos(x) |
real | $-1 \leq x \leq 1$ | Inverse Cosine function |
| $\tan^{-1} x$ | np.arctan(x) |
real | $-\infty \leq x \leq \infty$ | Inverse Tangent function |
The Inverse Sine Function
The inverse sine function is defined only when we restrict the domain of $\sin x$ to $[-\frac{\pi}{2},\frac{\pi}{2}]$ so that $\sin x$ is one-to-one. The inverse sine function is defined as follows:
$y= \sin^{-1}x \iff x = \sin y$
where $-1 \leq x \leq 1$ and $-\frac{\pi}{2} \leq y \leq \frac{\pi}{2}$
The $\sin x$ function and its inverse $\sin^{-1}x$ are plotted side by side in the following figure.
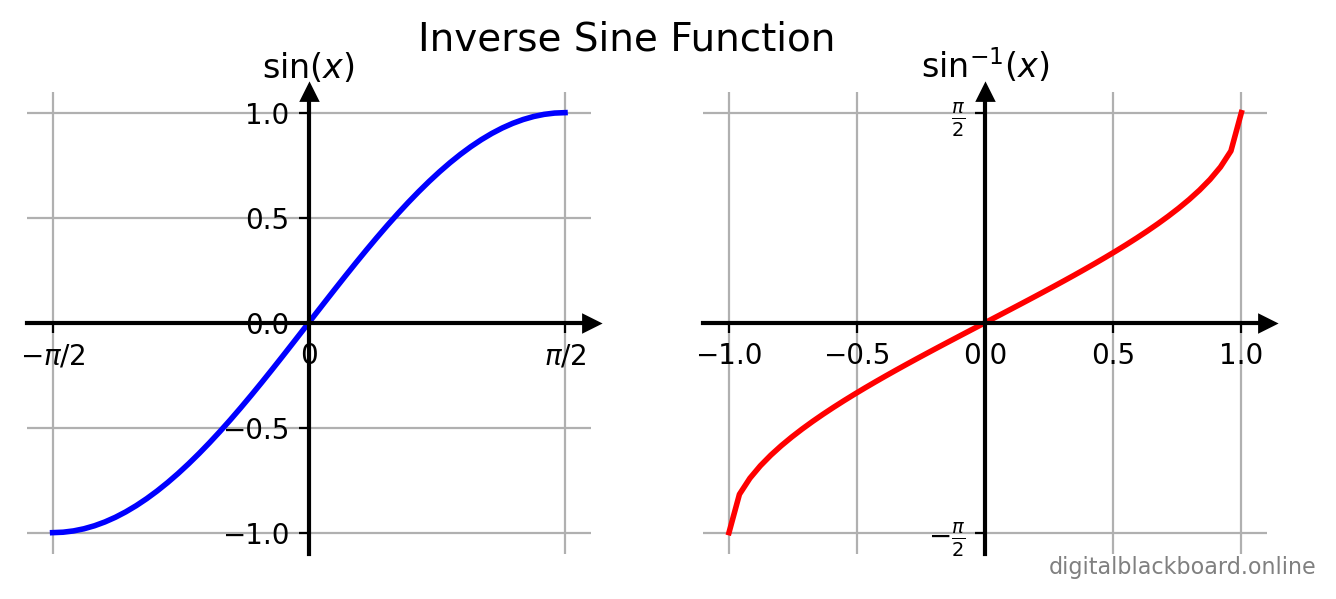
The inverse sine function can be computed using the NumPy ufunc np.arcsin(x).
Example
Computing the $\sin^{-1}x$ function.1import numpy as np
2x = np.linspace(-1, 1, 9)
3print(x) # x values
4print(np.around(np.arccos(x),3)) # arcsin values
[-1. -0.75 -0.5 -0.25 0. 0.25 0.5 0.75 1. ]
[-1.571 -0.848 -0.524 -0.253 0. 0.253 0.524 0.848 1.571]
The superscript $-1$ that appears in $y = \sin^{-1}x$ is not an exponent but the symbol used to denote the inverse function $f^{-1}$ of $f$. To avoid confusion, the notation $y = \text{Arcsin}~x$ may sometimes be used instead of $y = \sin^{-1}x$.
The Inverse Cosine Function
The inverse cosine function is defined only when we restrict the domain of $\cos x$ to $[0,\pi]$ so that $\cos x$ is one-to-one. The inverse sine function is defined as follows:
$y= \cos^{-1}x \iff x = \cos y$
where $-1 \leq x \leq 1$ and $0 \leq y \leq \pi$
The $\cos x$ function and its inverse $\cos^{-1}x$ are plotted side by side in the following figure.
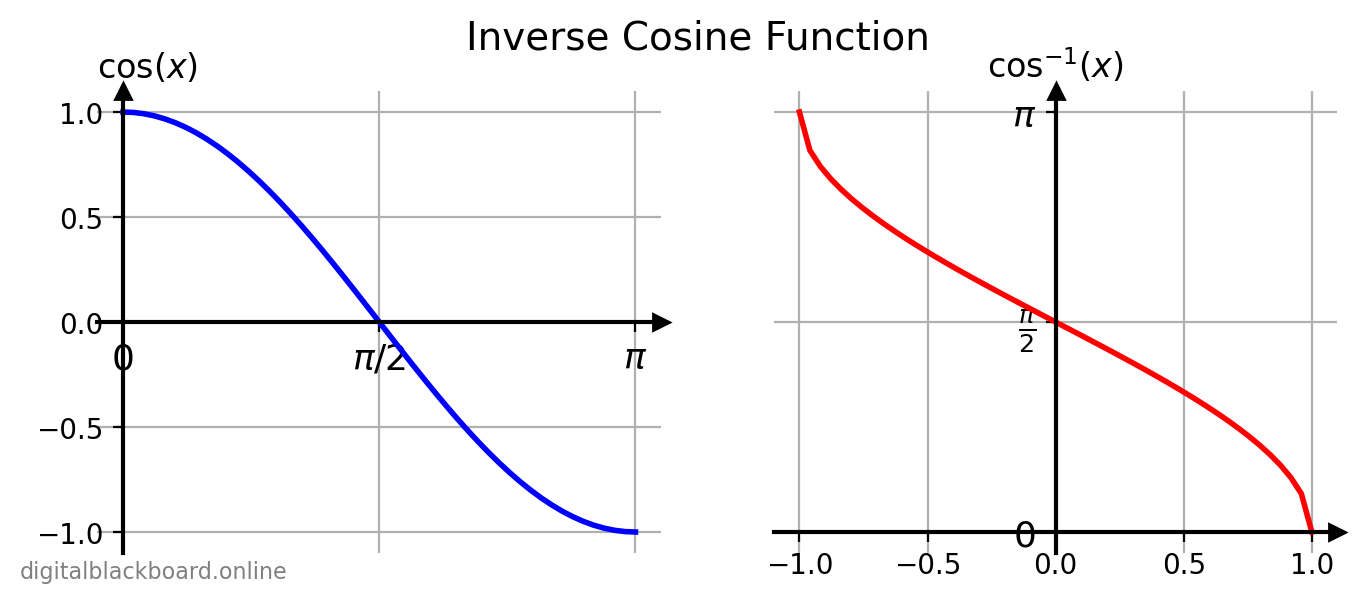
The inverse cosine function can be computed using the NumPy ufunc np.arccos(x).
Example
Computing the $\cos^{-1}x$ function.1x = np.linspace(-1, 1, 9)
2print(x) # x values
3print(np.around(np.arccos(x),3)) # arccos values
[-1. -0.75 -0.5 -0.25 0. 0.25 0.5 0.75 1. ]
[3.142 2.419 2.094 1.823 1.571 1.318 1.047 0.723 0. ]
ADVERTISEMENT
The Inverse Tangent Function
The inverse tangent function is defined only when we restrict the domain of $\tan x$ to $(-\frac{\pi}{2},\frac{\pi}{2})$ so that $\tan x$ is one-to-one. The inverse tangent function $y= \tan^{-1}x$ is defined as follows:
$y= \tan^{-1}x \iff x = \tan y$
where $-\infty < x < \infty~$ and $~-\frac{\pi}{2} < y < \frac{\pi}{2}$
The $\tan x$ function and its inverse $\tan^{-1}x$ are plotted side by side in the following figure.
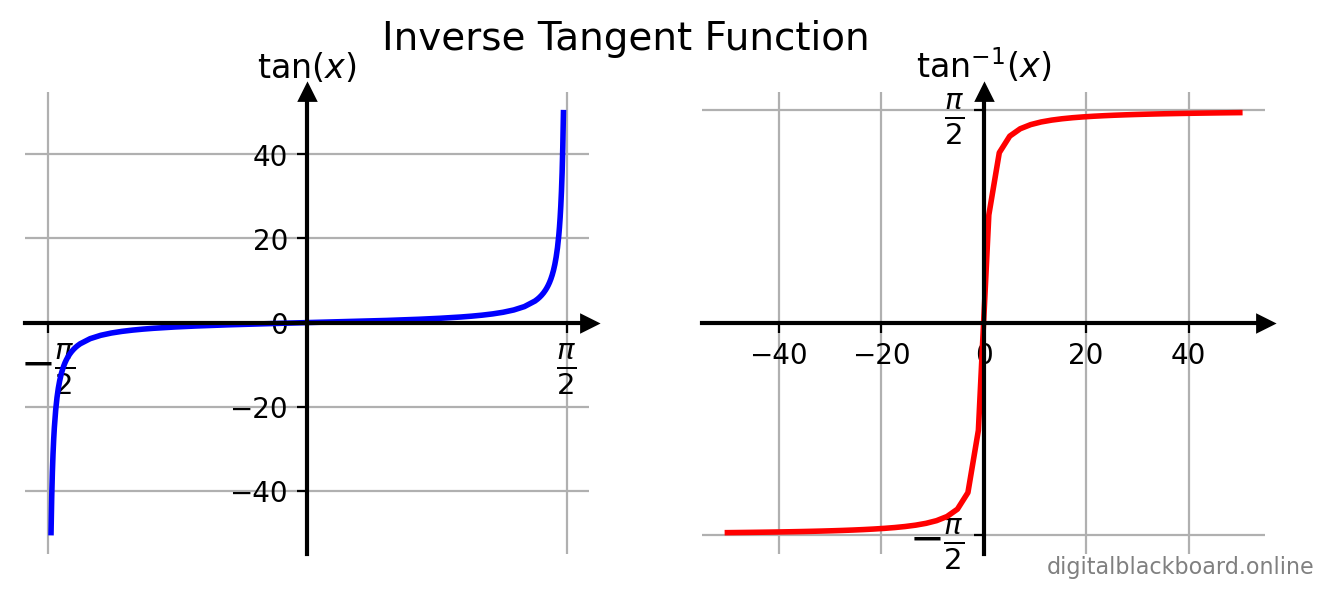
The inverse tangent function can be computed using the NumPy ufunc np.arctan(x).
Example
Computing the $\tan^{-1}x$ function.1x = np.linspace(-100, 100, 9)
2print(x) # x values
3print(np.around(np.arctan(x),3)) # arccos values
[-100. -75. -50. -25. 0. 25. 50. 75. 100.]
[-1.561 -1.557 -1.551 -1.531 0. 1.531 1.551 1.557 1.561]