Table of Contents

Introduction

Definition

The logarithmic function with base $a$ where $a>0$ and $a\ne1$ (denoted by $y=\log_a x$) is defined as:

$\boxed{y = \log_a x \iff x=a^y}$

where $x>0$ and $-\infty< y<\infty$.

The logarithmic function $\log_e x$ is available as the NumPy ufunc np.log(x). The NumPy ufuncs for commonly-used logarithmic functions are tabulated below.

Function NumPy Ufunc Special Name
$\ln x = \log_e x$ np.log(x) Natural logarithm
$\log_{10} x$ np.log10(x) Common logarithm
$\log_2 x$ np.log2(x) Binary logarithm
$\ln (1+x)$ np.log1p(x) -
$\log_b x= \frac{\ln x}{\ln b}$ np.log(x)/np.log(b) -

The natural logarithm $\log_{e} x= \ln x$ has the Euler’s number $e$ as its base and its use is widespread in mathematics and physics because of its simpler integral and derivative. The common logarithm $\log_{10} x$ uses base $10$ and is commonly used in science and engineering. Finally the binary logarithm $\log_{2} x$ uses base $2$ and is frequently used in computer science.

Computing the Logarithmic Function

Example

Computing the commonly-used logarithmic functions.

1import numpy as np
2x = np.linspace(0.1, 2, 5)
3print(x)
4print(np.log(x)) # base e
5print(np.log10(x)) # base 10
6print(np.log2(x)) # base 2
7print(np.log1p(x)) # log(1+x) base e

[0.1   0.575 1.05  1.525 2.   ]
[-2.30258509 -0.55338524  0.04879016  0.42199441  0.69314718]
[-1.         -0.24033216  0.0211893   0.18326984  0.30103   ]
[-3.32192809 -0.79836614  0.07038933  0.60880924  1.        ]
[-2.30258509 -0.55338524  0.04879016  0.42199441  0.69314718]

Computing the Logarithmic Function to any Base $b$

The logarithm $\log_b x$ to base $b>0, b\ne 1$ can be computed from the logarithms of $x$ and $b$ with respect to an arbitrary base $k$ using the following change-of-base formula.

$$\boxed{\log_b x = \frac{\log_k x}{\log_k b}}$$

Example

Computing the logarithmic function to base $2$.

1x = np.linspace(0.1, 2, 5)
2print(x)
3print(np.log2(x)) # base 2
4print(np.log(x)/np.log(2)) # base 2 using change of base

[0.1   0.575 1.05  1.525 2.   ]
[-3.32192809 -0.79836614  0.07038933  0.60880924  1.        ]
[-3.32192809 -0.79836614  0.07038933  0.60880924  1.        ]

We see that the results of the NumPy ufunc np.log2(x) are identical to those produced using the change-of-base formula (last array).

Example

Computing the logarithmic function to base $3$.

1x = np.linspace(0.1, 2, 5)
2print(x)
3print(np.log(x)/np.log(3)) # base 3 using change of base

[0.1   0.575 1.05  1.525 2.   ]
[-2.09590327 -0.50371295  0.04441072  0.38411587  0.63092975]
❓ Question Check that the above result is correct.
Answer Note that $y = \log_a x \iff x=a^y$. Therefore, we just need to check if $a^y$ returns the original array x. 
1print(x)
2y=np.log(x)/np.log(3) # base 3 using change of base
3print(y)
4print(np.power(3,y)) # check equal to x

[0.1   0.575 1.05  1.525 2.   ]
[-2.09590327 -0.50371295  0.04441072  0.38411587  0.63092975]
[0.1   0.575 1.05  1.525 2.   ]

ADVERTISEMENT

Plotting the Logarithmic Function

Let’s first import the relevant libraries and modules. In addition to the NumPy and Matplotlib libraries, the db_plot module consists of utility functions for plotting which will be discussed in more detail in our course on Plotting and Visualization with Matplotlib.

1import numpy as np
2import matplotlib.pyplot as plt
3import db_plot # module with plotting utilities

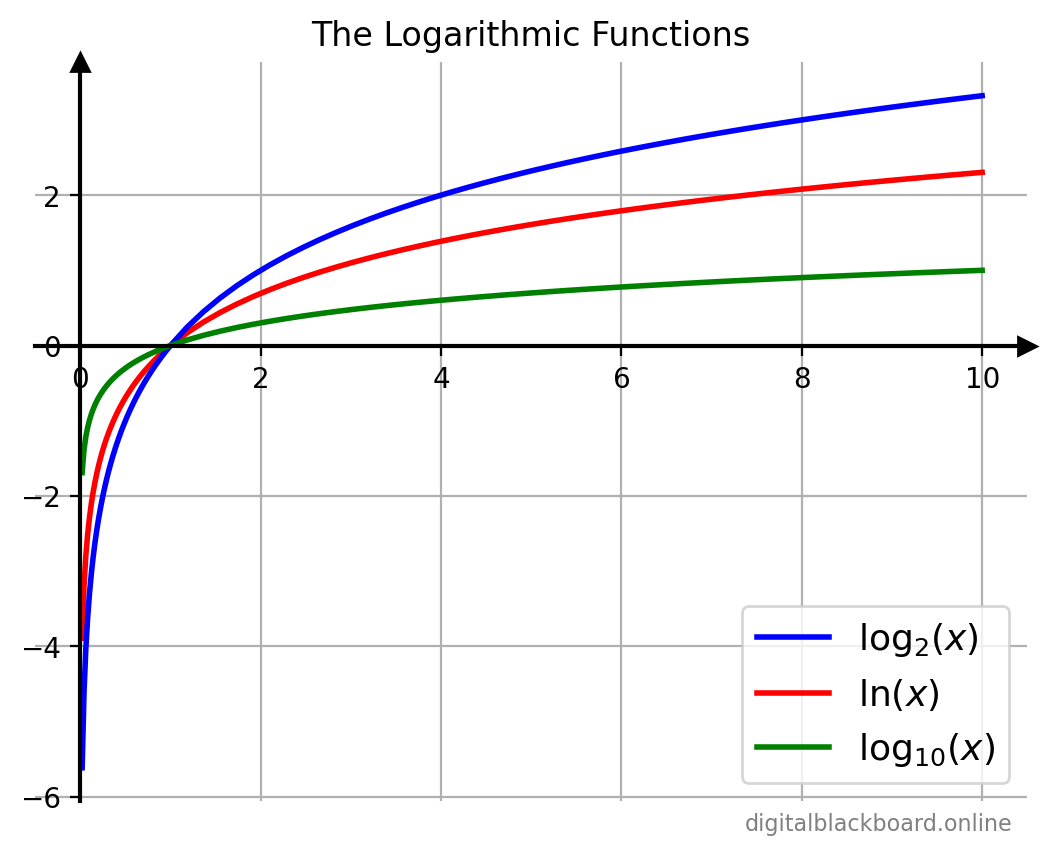
The logarithmic function $y=\log_a x$ is plotted for the various values of the base $a$.

Example

Graphs of $y=\log_a x$ for various $a$.

1x = np.linspace(0, 10, 100)
2fig, ax = plt.subplots(1)
3ax.plot(x, np.log(x), 'r-',   linewidth=2, label=r'$\ln(x)$')
4ax.plot(x, np.log2(x), 'b-',   linewidth=2, label=r'$\log_2 (x)$')
5ax.plot(x, np.log10(x), 'g-',   linewidth=2, label=r'$\log_{10}(x)$')
6db_plot.shiftAxes(ax,1) # ax, grid on
7ax.set(xlabel='', ylabel='', title='The Logarithmic Functions')
8plt.legend(loc="lower right")

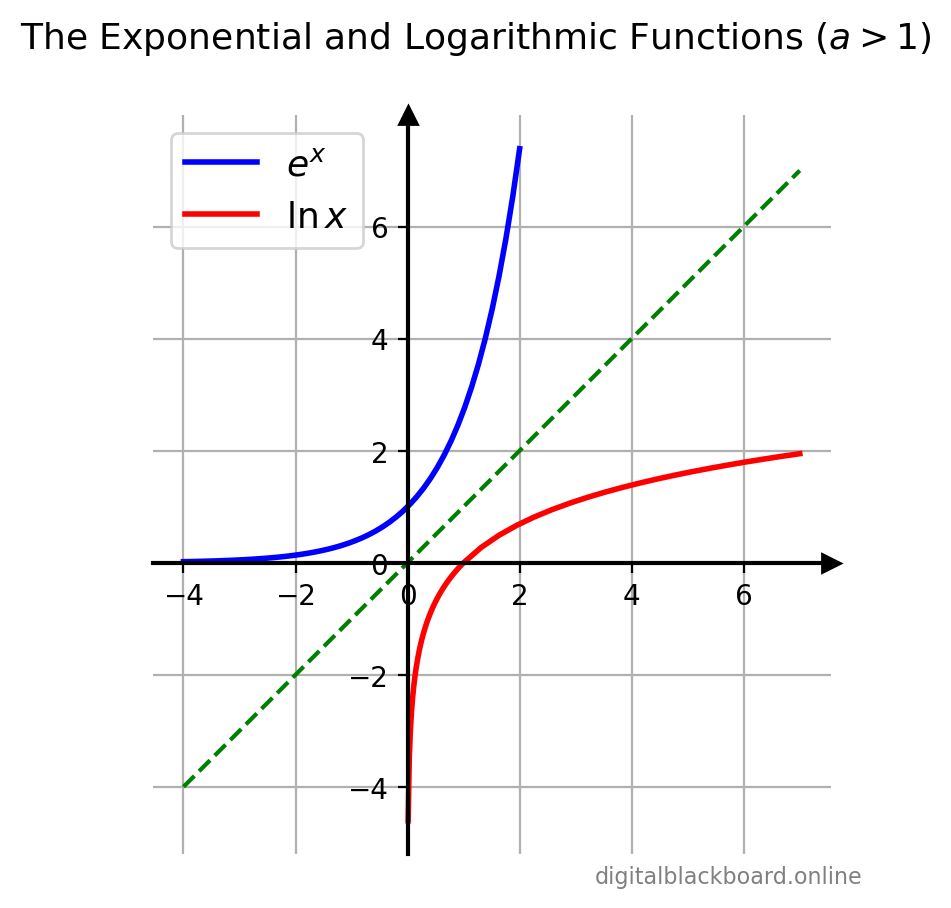
Since the logarithmic function $y=\log_a x$ is the inverse of the exponential function $y=a^ x$, it can be obtained from the graph of $y=a^ x$ by a reflection about the line $y=x$.